Research Highlights

Network Science

Synchronization Phenomena
Ageing Transitions in Phase Oscillators

Swarming Dynamics
Adaptive Networks

Population Ecology
Our Interest Areas
Cascading Failure and Mitigation in Complex Networks
In the intricate fabric of complex networks, the phenomenon of cascading failure looms as a critical challenge. Cascading failure occurs when the failure of a single component within the network triggers a domino effect, propagating through interconnected nodes and leading to widespread system breakdown. This dynamic process poses significant risks to various systems, from power grids and transportation networks to social media platforms and financial systems. Mitigating cascading failure demands a multifaceted approach, encompassing both proactive measures and reactive strategies. These may include enhancing network resilience through redundancy and robustness, implementing targeted monitoring and early warning systems, and developing adaptive control mechanisms to contain and mitigate the impact of failures. As we delve deeper into understanding the complexities of cascading failure, our quest for effective mitigation strategies remains paramount in ensuring the stability and resilience of interconnected systems.
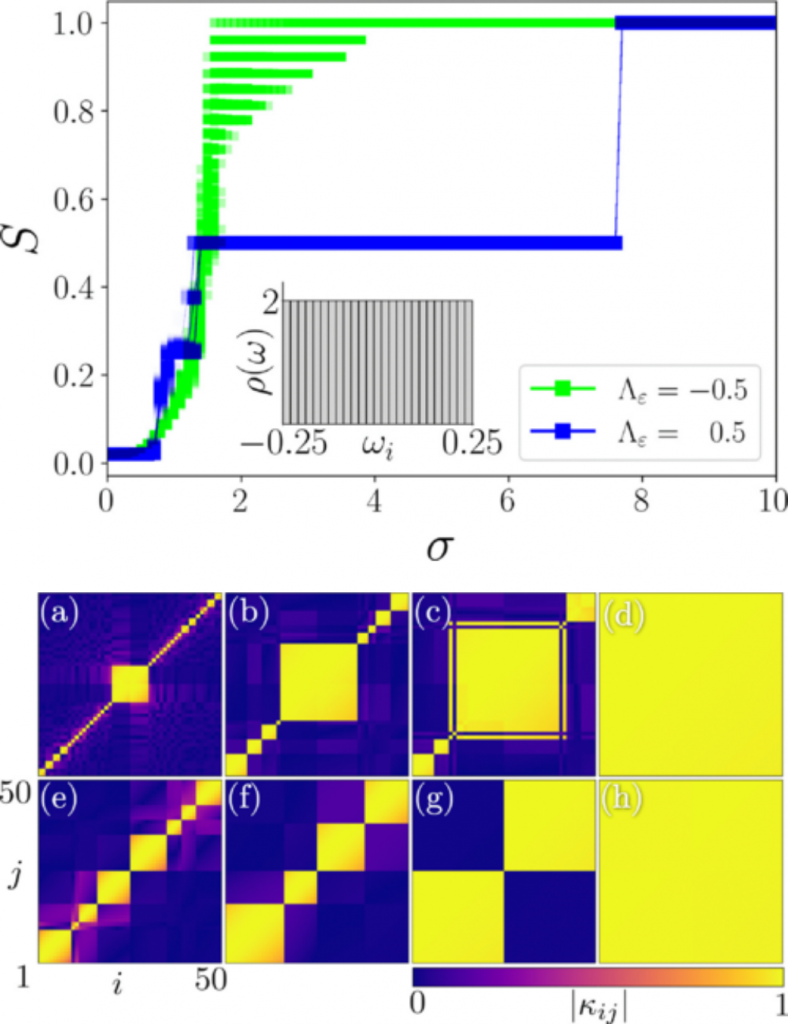
Synchronization Phenomena
Synchronization, a fundamental concept across various domains, entails the coordination of multiple elements to operate in harmony or alignment. From intricate biological processes to complex technological systems, synchronization plays a pivotal role in facilitating coherent and efficient operation. In communication systems, synchronization ensures accurate signal transmission and reception, while in distributed computing, it coordinates concurrent processes to maintain data integrity. Biological systems rely on synchronization for regulating essential functions like neuronal firing and circadian rhythms. As we delve deeper into understanding synchronization mechanisms, we uncover their critical significance in fostering stability and coherence across diverse systems. This introduction sets the stage for exploring the multifaceted aspects of synchronization and its pervasive influence in both natural and engineered systems.
Ageing Transitions in Phase Oscillators
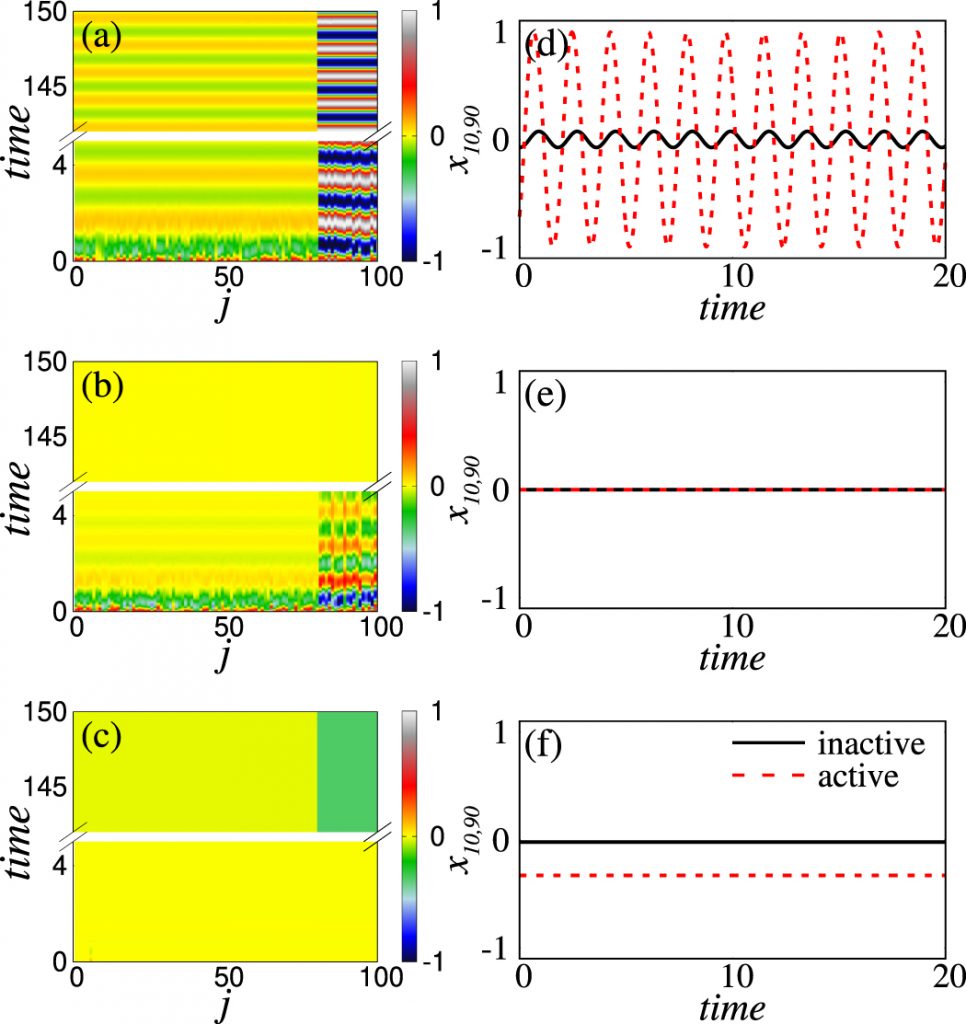
In networks of coupled oscillators, the aging transition refers to the evolution of collective behavior influenced by the gradual degradation of individual components. This phenomenon is studied using macroscopic order parameters derived under strong coupling conditions, which capture the overall dynamics of the network. The transition highlights how changes in the network’s structure and connectivity, influenced by factors like heterogeneity among oscillators and feedback mechanisms, affect its stability and functionality over time. Critical stability analysis based on these parameters identifies thresholds where the network shifts between different states, offering insights into its resilience and response to internal and external influences as it ages.
Swarming Dynamics
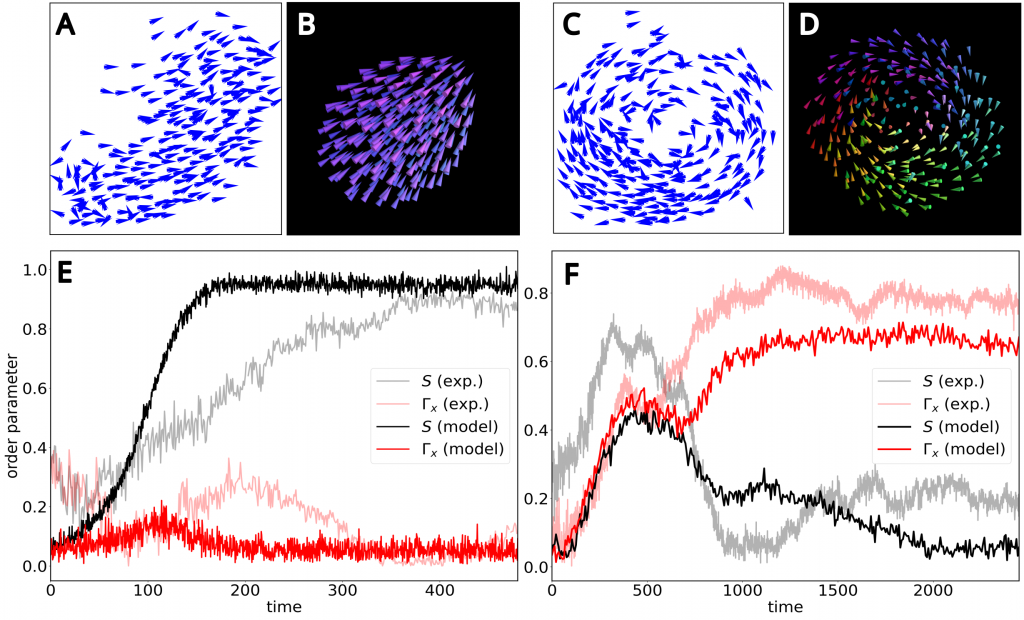
Swarming dynamics describes the collective behavior observed in groups of entities, whether animals, insects, or artificial agents, as they move together in a synchronized manner. Through simple local interactions, individuals within the swarm exhibit emergent behaviors such as flocking or schooling, without the need for centralized control. This phenomenon finds applications across diverse fields, including robotics and biology, where researchers explore swarming algorithms for tasks such as collective transport and navigation. Understanding swarming dynamics involves analyzing how individual interactions give rise to complex collective patterns. By leveraging these principles, researchers strive to design efficient and scalable systems for various applications, from distributed sensing to disaster response and urban planning.
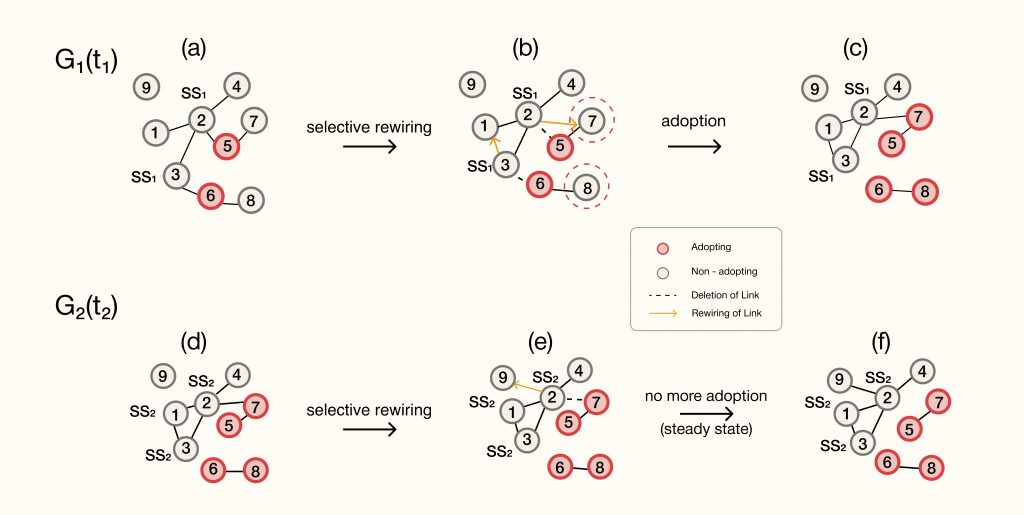
Adaptive Dynamic Networks

An adaptive dynamics network is a dynamic system comprised of interconnected nodes that continuously adapt their connections and behavior in response to changing circumstances. These networks differ from static ones by allowing for the evolution of connections over time, driven by feedback loops, environmental cues, or individual node interactions. By modeling the adaptive behavior of complex systems, such as biological networks or social structures, researchers gain insights into the emergence of patterns, resilience to disruptions, and the optimization of network performance. Adaptive dynamics networks serve as powerful tools for understanding the intricate interplay between structure and function in dynamic systems, guiding strategies for adaptation and intervention in diverse fields.
Population Ecology
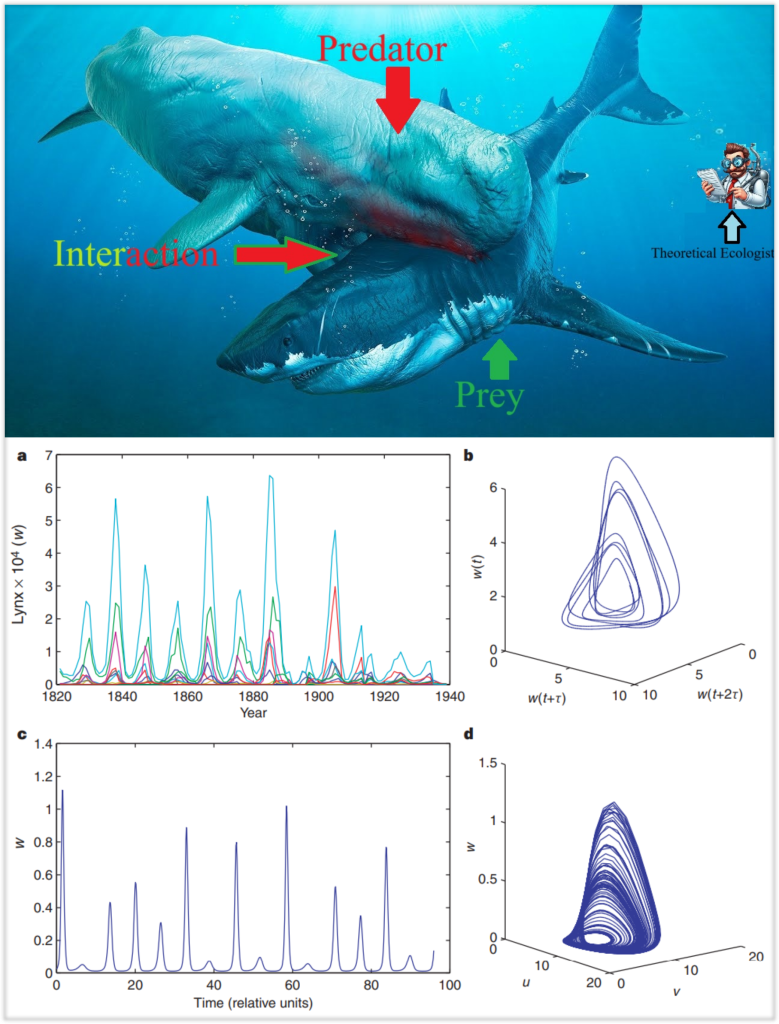
Population ecology is a cornerstone of computational biology and theoretical ecology, dealing with the biodiversity and persistence of an ecosystem primarily through the lens of spatio-temporal species population dynamics. Specific essential parameters, particular to the ecosystem in question, govern the population dynamics of an ecosystem and thus majorly influence the extinction risk of ecosystems. Such parameters quantify biotic and abiotic phenomena like the death rate of a species, the birth rate of a species, immigration, emigration, trophic and non-trophic interspecies and intraspecies interactions, as well as eco-environmental interactions, like climate change, habitat loss, and human influence. Factoring in these parameters, the population dynamics of ecosystems are described by prey-predator models, which are essentially nonlinear and can be analyzed using the robust structure of nonlinear dynamics. This fundamentally ‘physical’ approach to theoretical ecology has resulted in several remarkable observations and predictions (e.g., Figure 1. From Blasius and Stone, 1991). Not only do these models exhibit features of traditional nonlinear dynamics like chaoticity, but we can extend them readily to construct complex networks of food -webs ( i.e., multi-species oscillator models), which accurately describe the intricacies of a natural ecosystem. We live in ecosystems, and understanding what keeps them alive is what keeps us alive, and NLD can help us keep it that way.
About logo: The butterfly logo embodies the profound concept that complex and chaotic processes can give rise to astonishing beauty. Much like the intricate wings of a butterfly emerge from chaotic trajectories within a Lorenz attractor, our logo’s design symbolizes this convergence of chaos and creativity. The wings, crafted from the dynamic patterns of the Lorenz attractor, reflect the intricate dance of unpredictability. They are intricately connected to the main body, which represents a complex network, symbolizing the interconnectedness of diverse elements within our field. Together, these elements converge to create something truly beautiful, enriching our understanding of nature’s complexities and inspiring awe in its intricate design.
~ Karan & Akash